SPIの非言語は難しい?問題を解くコツや覚えるべき公式を紹介
2024年7月12日
 就活生 Aさん
就活生 Aさん
ネットで調べたらSPIの非言語は難しいと出てきたのですが、実際はどうなんでしょうか?
正直、SPIの非言語は難しいです!
 キャリアアドバイザー 岡田
キャリアアドバイザー 岡田
 就活生 Aさん
就活生 Aさん
そうなんですね。どのへんが難しんでしょうか?有効な対策法があれば教えてほしいです!
わかりました!
このコラムでは、SPI非言語の特徴や難しいといわれる理由と対策のコツについて解説します。参考にしてください!
 キャリアアドバイザー 岡田
キャリアアドバイザー 岡田
目次
SPIの非言語とは?

SPIの非言語とは、図形や記号などの情報を用いて、推論や分析能力が必要となる問題が出題される試験のことです。
SPIの基本情報や出題される分野については以下で詳しく説明します。
SPIの基本情報
SPIとは、Webテストの中で最もメジャーな試験です。多くの企業で採用されている試験のため、就活生は対策する必要があります。
SPIを実施する企業の目的は、受験者の性格や基本スペックを把握するためです。また、面接で性格などに矛盾がないか見極める判断材料にする目的もあります。
SPI試験は、言語・非言語・性格検査に分かれています。言語や非言語の難易度は、中学〜高校レベルです。しかし、問題数が多く、制限時間内に最後まで解くことが難しい試験です。
SPIの分野ごとの制限時間は以下の通りです。
| 検査 | 時間 |
|---|---|
| 非言語 | 約35分 |
| 言語 | 約35分 |
| 性格検査 | 約30分 |
今回はSPI非言語について紹介していきます。
SPI非言語で出題される分野
SPI非言語で出題される分野は以下の通りです。
- 順列・組み合わせ
- 推論
- 集合
- 割合
- 確率
- 損益計算
- 仕事算
- 速度
- 場合の数など
1つ1つの問題難易度は中学〜高校レベルですが、出題範囲が広いので、幅広く対策する必要があります。
就活ではSPI非言語についてはもちろん、webテストや自己分析、企業・業界研究など様々なことについて理解を深める必要があります。
そんな就活に対して疑問や不安を抱えている人は、キャリチャンの就活支援サービス「就活相談サポート」に参加してください。SPI非言語を始め、就活に対する悩みを解決します。ぜひプロのキャリアアドバイザーを頼ってください。
SPIの非言語が難しすぎるといわれる理由

ここでは、SPIの非言語が難しすぎるといわれる理由について解説します。
具体的な理由は以下の通りです。
問題自体の意味が難しい
SPIの非言語が難しすぎるといわれる理由の1つは、問題自体の意味が難しいことです。
問題自体の意味が難しいと、問題を理解できないため、正答率が下がります。その結果、点数が低くなり、非言語のテストが難しいと感じるのです。
例題は以下の通りです。
ある会社で140人の社員を対象に、昼食に食堂を利用する人と弁当を持参する人についてアンケートを取りました。
その結果、昼食に食堂を利用する社員は85人、弁当を持参する社員は45人いた。また、食堂の利用とお弁当の持参の両方をしている社員は30人であった。
このとき、食堂の利用とお弁当の持参以外の方法で昼食を取っている社員は何人いるだろうか。
- 10人
- 15人
- 20人
- 25人
- 30人
- 35人
- 40人
- 45人
〈解答〉
40人
初見では状況整理に時間がかかる問題が多いことから、SPIが難しすぎるといわれる理由になっています。
問題の意味はわかるけど解き方がわからない
問題の意味はわかるけど、解き方がわからないことで難しさを感じるケースもあります。SPIの非言語は、公式を覚えないと回答するのが難しい問題が多いです。
例題は以下の通りです。
箱の中にみかんが2個、りんごが8個入っている。
この中から同時に2個の果物を取り出すとき、りんご2個取り出す確率はいくらか。
- 3 / 8
- 13 / 45
- 8 / 35
- 28 / 45
- 28 / 35
- 23 / 45
- 17 / 35
- 19 / 45
〈解答〉
D 28/45
この問題を解くためには、組み合わせの公式を使わなくてはなりません。このような問題を難しいと感じる人は、公式をきちんと覚えられていないことが原因でしょう。
時間が足りない
時間が足りなくて、SPIの非言語は難しすぎると感じる人もいます。
SPI非言語はペーパーテストを除いて、1問あたり1分以内で答えなければなりません。また、推論の問題のように、状況把握をしてから解く必要がある問題は時間が足らなくなりやすいです。
さらに、WEBテストとテストセンターはSPIの非言語は1問ごとに時間制限があり、時間を過ぎると強制的に次の問題に進んでしまいます。
これらの状況がSPI非言語の難易度を引き上げています。
公式を覚えなければ解けない問題が多い
公式を覚えなければ解けない問題が多いのも、SPIの非言語は難しすぎるといわれる理由の1つです。自己流で解こうとしても、問題を解くことは難しいです。
一方、公式を覚えれば柔軟に対応できるようになり、解答スピードも上がるのでSPIの通過率を上げられます。
そのため、SPIの非言語問題の苦手意識をなくすためには、公式を覚える必要があるでしょう。
SPI非言語の基本の対策法

ここでは、SPI非言語の基本の対策法について解説します。
対策法は以下の通りです。
以上の内容はSPI非言語の共通していえる対策法なので、以下で紹介する「【種類別】SPIの非言語問題の対策方法」と合わせてご覧ください。
SPI非言語で使える公式を覚える
前の項でもお話ししたように、SPIの非言語を攻略するためには、公式を覚えることが大切です。
SPIの非言語で使える公式一覧表は以下の通りです。
| 問題 | 公式 |
|---|---|
| 速さ・時間・距離 |
|
| 集合 | ベン図の理解 |
| 平均世帯人数 | 平均世帯人数=世帯人数の合計÷世帯数 |
| 仕事算 | それぞれかかる日数を分母にして足す |
| 割合 |
|
| 損益算 |
|
| 通過算→トンネル通過 | 時間=(列車+トンネルの長さ)÷速さ |
| 通過算→すれ違う | 時間=列車の長さの合計÷速さの和 |
| 通過算→追い越す | 時間=列車の長さの合計÷速さの差 |
| 流水算 |
|
| 組み合わせ(順番考慮なし) |
nCr=nPr÷r! ={n(n−1)(n−2)⋯⋯(n−r+1)}÷{r(r−1)⋯⋯3×2×1} |
| 組み合わせ(順番考慮あり) |
nPr=n(n−1)(n−2)⋯⋯(n−r+1) =n!÷(n−r) |
| N進法 | Nの数字でわり続ける |
| 確率 |
|
以上の公式を覚えれば、非言語の問題に答えやすくなり、スムーズに試験を受けられるようになるでしょう。
出題頻度の多い分野を抑える
出題頻度の高い分野を抑えるのも、SPI非言語対策のポイントです。具体的な分野は、推論・確率・図表の読み取り・集合です。
これらの問題の公式を覚え、繰り返し問題を解くようにしましょう。そうすれば、多少問題文が違ってもある程度対応できるため、点数を稼げます。
ただし、推論に関しては決まった公式がないので、反復練習で問題に慣れるのがよい対策法です。
1冊の問題集を繰り返し解く
1冊の問題集を繰り返し解くことも、SPIの非言語の対策法です。SPIの非言語は、解き方さえ覚えられれば、ほとんどの問題に対応できます。
つまり、1冊の参考書を反復練習して解き方を完璧にするのが、SPIの非言語の対策になるのです。
オススメの問題集は以下の通りです。
それぞれの参考書の特徴について説明します。
「史上最強SPI&テストセンター超実戦問題集」は、早く問題を解くコツが徹底的に記載されているため、高い点数を目指す人にオススメの参考書です。
「7日でできる!SPI[頻出]問題集」は、出題される確率の高い問題を多く扱っているため、卒論で忙しい人や勉強の時間を多くとれない人にオススメの参考書です。
「これが本当のSPI3だ! 」は、WEBテスト、テストセンター、ペーパーテストの3種類すべてに対応しています。
また、問題が多く掲載されているので、SPIについて広く勉強したい人にオススメの参考書です。SPIの対策状況は人それぞれなので、自分の状況に合わせて参考書を選びましょう。
模擬試験を受ける
模試を受けるのも、SPI非言語の対策法の1つです。
模擬試験は本番を想定した形で試験を受けることができるため、力をつけやすいです。また、試験において重要な時間配分も、模擬試験を通して定めることができるため、対策として有効的です。
さらに、現在の実力を試せるので、点数がよければ自信につながるというメリットもあります。解けなかった問題を家に帰ってから復習できるので、インプットしやすくなるでしょう。
それでも、うまく一人で対策ができない、SPI非言語どころか就活もうまくいかないと悩む人は、キャリチャンの就活支援サービス「就活相談サポート」に参加してください。webテストに集中できるよう、就活全般のサポートを行います。
【種類別】SPIの非言語問題の対策方法

ここまでSPI非言語における共通の対策法を紹介しました。ここからは、SPI非言語の種類別の対策法について解説していきます。
SPI非言語の種類は以下の通りです。
また、キャリチャンではSPIの問題集を配布しているので、ぜひご活用してください。
【就活対策資料】
SPI解説付き問題集
順列・組み合わせの問題
順列・組み合わせの問題は、まず公式を覚えてから、どちらに分類されるか把握する必要があります。
順列と組み合わせの問題は似ていますが、使う公式は異なります。順列の公式は、「nPr=n! / (n−r)!」です。一方、組み合わせの公式は、「nCr」です。
今回は順列の公式を使う例題を紹介します。
A、B、C、Dが書かれた4枚のカードがある。
この4枚から3枚を並べて3桁の整数を作るとき、何通りの作り方があるか。
- 3通り
- 6通り
- 12通り
- 24通り
- 36通り
- 48通り
- 60通り
- 120通り
- 24通り
「順列」の理解を深めるために、1ステップずつ丁寧に解説する。
- 4枚のカードから1枚を取り出して、1桁の整数を作ることを考えると、この作り方は4通りある。
- 4枚のカードから2枚を取り出して、2桁の整数を作ることを考えると、4×3=12(通り)ある。
- 4枚のカードから3枚を取り出して、3桁の整数を作るときは、4×3×2 = 24(通り)
問題文を順列の公式に当てはめると、同様に24通りと答えが出る。
推論の問題
推論は非言語の中でも難しいといわれています。なぜなら、公式がないからです。
そのため、練習問題をたくさん解くことで、問題の傾向に慣れるための対策をする必要があります。また問題を解く際は、状況を整理するために紙に書き出したり、図や表にしたりするとよいです。
以下で例題を紹介します。
薬局、八百屋、本屋、雑貨屋に、A、B、C、Dの4人が2店ずつ買い物に行った。1〜4が次のように語ったとき、正しいものは次のうちどれか。ただし、A、B、C、Dの4人が、3人以上同じ店に揃うことはない。
- 「私は本屋でAとDに会った」
- 「私とCとBが雑貨屋に行った」
- 「私はAとCに八百屋で会った
- 「私はBとDに薬局で会った」
選択肢
- ア:Aは薬局に行った
- イ:Dは雑貨屋に行った
- ウ:Aは八百屋に行かなかった
- エ:Bは本屋に行かなった
〈解答〉
エ:Bは本屋に行かなかった
集合の問題
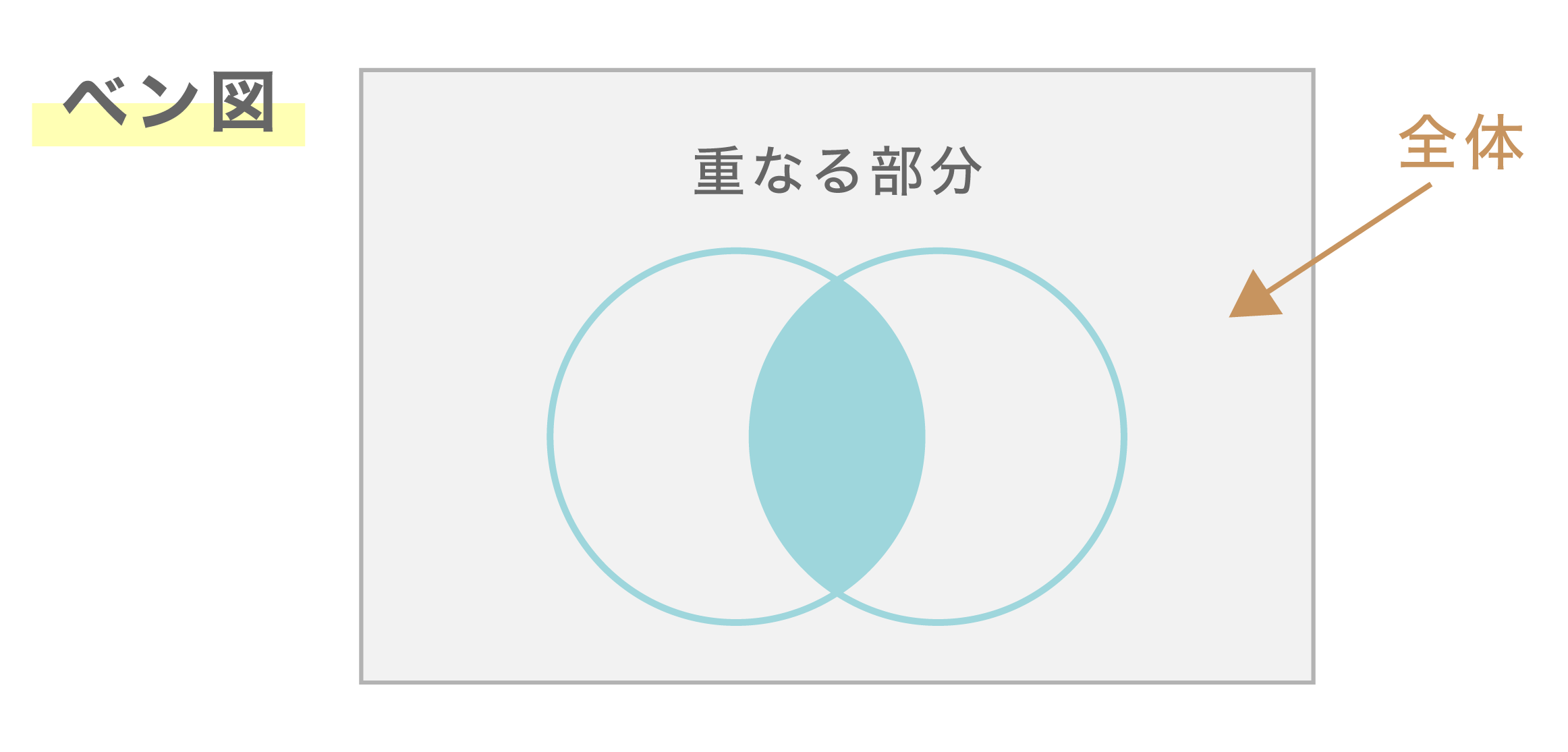
集合の問題は、ベン図を使うのがベストな選択になります。ベン図を使えば、どの部分が重なっているか、すぐにわかります。
ベン図とは、以下のようなものです。
例題を以下で紹介します。
外国人40人にアンケートをおこなったところ、英語が話せる人は24人、中国語が話せる人は8人、ドイツ語が話せる人は12人いた。
英語と中国語の両方が話せる人が5人いた。
英語と中国語のどちらか片方だけ話せる人は何人か。
ただし、ドイツ語は関係ないものとする。
〈解答〉
22人
ベン図は少し大きめに書くとよいです。大きめに書くことで情報を整理しやすくなり、ミスを減らせます。
割合の問題
割合の問題は、公式を覚え、問題に当てはめて考えるのが対策法です。まずは、割合の問題の公式「求める数=全体×割合」を覚えましょう。
また、比較的簡単な問題になるので、ほかの就活生に差をつけられないためにも、ミスをなくせるようにすることが重要です。
割合の例題を以下より紹介します。
ある一定期間の博物館の来場者は6000人であった。
そのうち40%が女性、60%が男性であった。
また、男性の来場者のうち、70%が20歳以上であった。
男性の来場者のうち、20歳未満の人数は何人か。
選択肢
- 880人
- 980人
- 1080人
- 1180人
- 1280人
- 1380人
- 1480人
- 1580人
〈解答〉
C:1080人
割引の問題
割合の問題は、2つの公式を覚えれば対応できます。ただし、どちらを使うのが適切か判断する必要があります。
2つの公式は以下の通りです。
【公式1】
割引率=(1-(割引後の価格÷元の価格))×10
【公式2】
売価=定価×(1-割引率)
今回の例題では、公式2を使って解く問題を紹介します。
ワンピースを定価の3割引の5,145円で売りました。
ワンピースの定価はいくらになるか。
- 6,430円
- 6,750円
- 7,000円
- 7,075円
- 7,350円
- 7,800円
- 8,080円
- 8,350円
〈解答〉
E 7,350円
〈解説〉
【公式を使って解く】
[ 売価 ] = [ 定価 ]×(1 – [ 割引率 ])を使って、定価を求める。
式)[ 売価 ] = [ 定価 ]×(1 – [ 割引率 ])
5145 = [ 定価 ]×(1 – 0.3)
5145 = [ 定価 ]×0.7
5145 ÷0.7 = [ 定価 ]
7350 = [ 定価 ]
[ 定価 ] = 7,350(円)
仕事算の問題
仕事算とは、1人が一定時間にした仕事量を求める計算のことです。仕事算を解くコツは、分母をそろえる点と全体を1として考えることです。
仕事算は、慣れるまで繰り返し解く必要がありますが、慣れればそこまで難しい問題ではありません。
例題を紹介します。
5日間でドラマを1話から最終話まで見ることにした。1日目に全体の1/5を、2日目に全体の2/7を見た。残りのドラマを3日間で見るとすると、1日あたりに見るのは全体のどれだけにあたるか求めよ。
〈解答〉
6/35
〈解説〉
全体を1とおいてみます。1日目に全体の1/5を、2日目に全体の2/7を見たので、
見たドラマは1/5 + 2/7=17/35より、残りのページは1 – 17/35=18/35となります。
これを3日間で均等に分けると、1日あたり18/35 ÷ 3=6/35(答)となる。
時間の問題
速度の対策法は、公式にあてはめることです。速度の公式は、時間=距離÷速さになります。
ただし、距離を求める場合は、距離=時間×速さのように形が変わるので注意してください。
また、秒で答える問題なら1分→60秒のように、単位をそろえることでミスを減らせます。時間を求める例題は以下の通りです。
長さ210mの電車が、時速108kmで信号機を通過する。
電車の最前部が信号機を通過し始めてから、最後部が通過し終えるまで何秒かかるか。
ただし、信号機の太さは考えないものとする。
- 2秒
- 3秒
- 4秒
- 5秒
- 6秒
- 7秒
- 8秒
- 9秒
〈解答〉
7秒
〈解説〉
秒数を求める問題なので、「△△(km / 時)÷3.6 = ○○(m / 秒)」を使って、時速を秒速に変換しておこう。
式)108÷3.6 = 30(m / 秒)よって、かかる時間は、
式)[ 時間 ] = [ 距離 ]÷[ 速さ ]
= 210÷30
= 7(秒)
年齢の問題
年齢の問題の対応策は、鶴亀算という公式を使うことです。鶴亀算とは、鶴と亀を足した合計の数とその足の総数から、それぞれの数を求める公式です。
どこをXに仮定して問題を解くかが重要になります。
例題は以下の通りです。
現在、母は50歳で子供は20歳である。母の年齢が子供の2倍になるとき、子供は何歳になっているか求めよ。
〈解答〉
30歳
〈解説〉
a年後に母の年齢が子供の2倍になるとしましょう。すると、50+a=2(20+a)という方程式が立てられます。
これを解くとa=10となるので、10年後の子供の年齢は20+10=30歳になります。
SPI非言語で出題される問題はたくさんありますが、きちんと対策していかないとwebテストを通過できません。そうならないためにも、しっかりと対策していきましょう。
もし、一人でうまく対策できない、webテストの対策で手一杯で他の対策ができない、と悩む人はキャリチャンの就活支援サービス「就活相談サポート」に参加してください。プロのキャリアアドバイザーが企業紹介や自己分析などのサポートを行います。
SPIの非言語でわからないことがあればキャリアアドバイザーに相談を
このコラムでは、SPIの非言語の共通対策法や種類別の問題を解くコツについて解説しました。SPIの非言語は対策をしっかりすれば、対応可能な試験であるため準備が大切になります。
具体的には、出題範囲で活用できる公式を覚えたり、普段から時間を計測したりすることです。このような準備ができていれば、SPIの非言語は難しすぎると感じることは少なく、むしろ得意になるはずです。
最後まで読んでも、SPIの非言語についてわからなかった人は、キャリアアドバイザーに相談してみてください。キャリアアドバイザーがあなたの悩みを解決してくれるでしょう。
「就活相談サポート」に参加しよう!
この記事の監修者

岡田 章吾
株式会社ジールコミュニケーションズ
HR事業部マネージャー
2014年に入社後、人材業界に10年間携わる。企業向けの採用コンサルティングを経て現在に至る。これまでに大手企業含めた150社の採用支援と、3,000人以上の就職支援を担当。
就活支援の得意分野は「書類・動画選考の添削」。特に大手企業のエントリーシートや動画選考に強みを持つ。これまで大手企業を中心に、「1,000名、150社以上」の書類・動画選考突破を支援した実績を持つ。
またこれらの知見を活かして学校におけるキャリアガイダンス セミナー内容の監修、講師を務めるなど、幅広くキャリア育成に尽力している。















































